Fractional Fourier shift

Back to Blog

03.03.2016 (20.03.2016)

Pick a sequence of points $\{x_n \in \TC : n \in [-M, +M]_{\TZ} \}$, and interpret them as points in $\TR^2$. We would like to make sense of a fractional periodic shift for the sequence $x$, which looks like this:

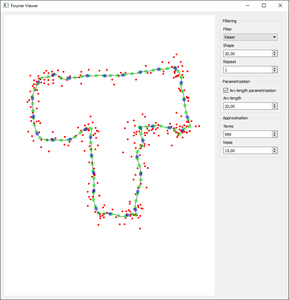
The sequence $x$ is denoted by red points, while its arc-length reparametrization is denoted by green points. The black curve is the continuous curve reconstructed from the green points. The moving blue circles visualize the parametrization of the black curve.

Motivation: Fourier descriptors

A Fourier descriptor is computed from the Fourier-series of an interpolating curve for $x$ by normalizing the desired geometric properties. A shape, given by its boundary, can then be searched among other shapes based on its Fourier descriptor, no matter what translation, scale, rotation, or fractional shift.

Property	Normalized Fourier-series coefficient
Translation invariance	$\hat{c}_0 = 0$
Rotation invariance	$\hat{c}_k = c_k / e^{i (\arg{c_1} + \arg{c_{-1}}) / 2}$
Fractional-shift invariance	$\hat{c}_k = c_k / e^{i k (\arg{c_1} - \arg{c_{-1}}) / 2}$
Scale invariance	$\hat{c}_k = c_k / \lvert c_r \rvert$,

where $r \in \TZ \setminus \{0\}$ is the index of Fourier-series coefficient with largest absolute value.

We demonstrate here that it is essential to take care of both noise-reduction and arc-length reparametrization before normalizing the fractional-shift.

Fractional shift

Shift of a periodic function

A shift of a periodic function $f : \TR \to \TC$ is a translation with $\delta \in \TR$:

$$\begin{align}f_{\delta}(t) = f(t - \delta).\end{align}$$

A shift is fractional if $\delta \not\in \TZ$.

We compute the shift by taking the Fourier-series transform (FST) of $f$, multiplying the Fourier-series coefficients by certain linear-phase exponentials, and then taking the inverse Fourier-series transform (IFST).

Shift of a finite sequence

We are studying a sequence $x$ for which the intermediate points are not explicitly defined.

To rotate the index of the sequence $x$, we take the discrete Fourier transform (DFT) of $f$, multiply the Fourier-transform coefficients by certain linear-phase exponentials, and take the inverse discrete Fourier transform (IDFT).

While a priori this process is defined only for integers, the mathematics allows us to specify a fractional shift. If we blindly attempt this, the drawn result seems not to generalize the shift geometrically.

However, a small change on the linear-phase exponentials fixes the problem. Why is this? How can a discrete sequence encode information about a continuous curve? We answer these questions by showing the following:

• The fractional-shift process implicitly reconstructs a continuous periodic function $f$ with a finite Fourier series.
• The DFT is an efficient way to compute the Fourier-series coefficients of $f$.
• The IDFT is an efficient way to uniformly sample $f$.

Reconstruction

We construct a smooth, periodic, band-limited $f : \TR \to \TC$, which interpolates the $x$-sequence on the interval $(-l, +l)$ by

$$\begin{align}f(t) = \sum_{n = -M}^M x_n h_n(t).\end{align}$$

where $h_n : \TR \to \TC$ is such that

$$\begin{align}h_n(t) = \frac{1}{2 M + 1} \sum_{k = -M}^M e^{i 2 \pi k \frac{t - t_n}{2l}}\end{align}$$

and

$$\begin{align}t_n = \frac{n}{2 M + 1} 2l.\end{align}$$

Orthogonal basis

We define an inner-product on the interval $(-l, +l)$ by

$$\begin{align}\left\langle f, g \right\rangle = \int_{-l}^{l} f(x)\overline{g(x)} \; \mathrm{d}x,\end{align}$$

which induces the $L2$-norm on $(-l, +l)$ by

$$\begin{align}\lVert f \rVert = \sqrt{\left\langle f, f \right\rangle}.\end{align}$$

The $\{h_n : n \in [-M, +M]_{\TZ}\}$ form an orthogonal basis for their span under this inner-product.

Relation to sinc-reconstruction

We rewrite the $h_n$ as

$$\begin{align}h_n(t) = \frac{1}{2 M + 1} \frac{\sin((2 M + 1) \pi (t - t_n) / (2l))}{\sin(\pi (t - t_n) / (2l))},\end{align}$$

taking limits where appropriate. This reveals the interpolatory behaviour

$$\begin{align}f(t_n) = x_n.\end{align}$$

The $h_n$ somewhat resembles the classical $\text{sinc}$-reconstruction function for non-periodic functions:

$$\begin{align}\text{sinc}(x) = \begin{cases} \frac{sin(\pi x)}{\pi x}, & x \neq 0, \\ 1, & x = 0. \end{cases}\end{align}$$

However, $\text{sinc}$-reconstruction is only applicable to functions of finite $L2$-norm on $\TR$, which excludes non-zero periodic functions.

Instead, the $h_n$ is the analogous interpolation function to reconstruct an $M$-bandlimited finite-L2-norm periodic function from uniformly-spaced samples; see S. Goldman, Information Theory, Prentice Hall, New York, 1953.

Finite Fourier series

We rewrite the expression for $f$ as a finite Fourier series

$$\begin{align}f(t) = \sum_{k = -M}^{M} d_k e^{i 2 \pi k \frac{t}{2l}},\end{align}$$

where

$$\begin{align}d_k = \frac{1}{2 M + 1} \sum_{n = -M}^M x_n e^{-i 2 \pi k \frac{n}{2 M + 1}} \\\end{align}$$

This shows that

$$\begin{align}f = \text{IFST}(d^*),\end{align}$$

where $d^*$ is the sequence $d$ zero-extended to a sequence in $\TZ$. This immediately provides the Fourier series of $f$, and shows that $f$ is $M$-bandlimited.

Fourier series coefficients by the discrete Fourier transform

We rewrite the Fourier-series coefficients $d$ as

$$\begin{align}d_k = \frac{1}{2 M + 1} \sum_{n = 0}^{2M} (x \circ s_M)_n e^{-i 2 \pi k \frac{n}{2 M + 1}},\end{align}$$

where $s_L : [0, 2L] \to [-L, +L]_{\TZ}$ is such that

$$\begin{align}s_L(n) = (n \text{ mod } (2L + 1)) - L.\end{align}$$

This shows that

$$\begin{align}d = \text{DFT}(x \circ s_M).\end{align}$$

Sampling by the inverse discrete Fourier transform

Let

$$\begin{align}u_n & = \frac{n}{2 N + 1} 2l, \\ y_n & = f(u_n - \delta),\end{align}$$

where $N \in \TZ^{\geq M}$, $n \in [-N, +N]_{\TZ}$, and $\delta \in \TR$. By definition, we have that

$$\begin{align}y_n & = \sum_{k = -M}^{M} d_k e^{i 2 \pi k \frac{u_n - \delta}{2l}} \\ {} & = \sum_{k = -M}^{M} \left( d_k e^{-i 2 \pi k \frac{\delta}{l}} \right) e^{i 2 \pi k \frac{n}{2N + 1}}.\end{align}$$

Depending on the value of $N$, we now divide into two cases: oversampling $(N \geq M)$, and undersampling $(N < M)$. The distinction exists only because we want perform the sampling by IDFT for efficiency.

Oversampling

For the oversampling case $N \geq M$,

$$\begin{align}y_n = \sum_{k = -N}^{N} c_k e^{i 2 \pi k \frac{n}{2N + 1}},\end{align}$$

where

$$\begin{align}c_k = \begin{cases} d_k e^{-i 2 \pi k \frac{\delta}{2l}}, & k \in [-M, +M]_{\TZ}, \\ 0, & \text{otherwise}. \end{cases}\end{align}$$

We rewrite the $y_n$ as

$$\begin{align}y_n = \sum_{k = 0}^{2N} (c \circ s_N)_k e^{i 2 \pi k \frac{n}{2N + 1}}.\end{align}$$

This shows that

$$\begin{align}y = \text{IDFT}(c \circ s_N).\end{align}$$

That is, adding zero-coefficients can be used to increase the number of samples.

Undersampling

For the undersampling case $N < M$, the extra coefficients sum into the lower coefficients:

$$\begin{align}y_n = \sum_{k = -N}^{N} c_k e^{i 2 \pi k \frac{n}{2N + 1}},\end{align}$$

where

$$\begin{align}c_k = e^{-i 2 \pi k \frac{\delta}{2l}} \sum_{i = \left\lceil \frac{-M-k}{N} \right\rceil }^{\left\lfloor \frac{M - k}{N} \right\rfloor} d_{k + iN}.\end{align}$$

This shows that

$$\begin{align}y = \text{IDFT}(c \circ s_N).\end{align}$$

Fractional shift

To summarize, the previous shows that the fractional shift of $x \in \TC^{[-M, +M]_{\TZ}}$ by $\delta \in \TR$, resampled to $x \in \TC^{[-N, +N]_{\TZ}}$, where $N \in \TZ^{\geq M}$, is achieved by

$$\begin{align}d & = \text{DFT}(x \circ s_M), \\ c_k & = \begin{cases} d_k e^{-i 2 \pi k \frac{\delta}{2l}}, & k \in [-M, +M]_{\TZ}, \\ 0, & k \in [-N, +N]_{\TZ} \setminus [-M, +M]_{\TZ}, \end{cases}, \\ y & = \text{IDFT}(c \circ s_N),\end{align}$$

where $s_L : [0, 2L] \to [-L, +L]_{\TZ}$ is such that

$$\begin{align}s_L(n) = (n \text{ mod } (2L + 1)) - L.\end{align}$$

Ringing and Gibb’s phenomenon

Using fractional shifting, we may now draw the reconstruction curve $f$ efficiently and in a numerically stable manner.

We then observe that $f$ exhibits ringing; $f$ is wavy in both transversal and longitudinal directions. In addition, when the sequence $x_n$ contains a jump, the point moves fast towards the next point, overshoots it, oscillates around it, and then dampens back to smoother behavior. This latter behavior is called Gibbs phenomenon.

We would like to eliminate the ringing. We do this by resampling the polygonal boundary defined by the sequence $x$ at unit-length intervals in time (green points). We call this (approximate) arc-length reparametrization.

Noise

When the points are corrupted by noise, the reconstruction curve starts to curl.

This is a consequence of requiring the curve to pass through all the points in order. We remove the curling by filtering the high-frequency components before arc-length reparametrization or approximation. This recovers the underlying curve, assuming the curve itself does not contain high-frequency components, such as sharp turns.

General filtering

We choose a filter function $G \colon \TR \to \TR$ to smooth out the curve. The filtered Fourier series coefficients are then given by

$$\begin{align}\hat{c}_k = c_k G(k / M)^p,\end{align}$$

where $p \in \TN$ is how many times the filtering is repeated. Denote the inverse Fourier-series transform of the coefficients $G(k / M)$ by $g \colon \TR \to \TR$. Then the filtering is equivalent to replacing the curve $f$ with

$$\begin{align}\hat{f} = f \ast (g \ast \cdots \ast g), \end{align}$$

where $g$ is convolved with itself $p - 1$ times. By eliminating the noise we lose the interpolation property — $\hat{f}$ interpolates the local average of $f$ instead. This is exactly what we wanted.

Lanczos filtering

One of the most popular filters is given by the Lanczos filter

$$\begin{align}G_L(x) = \begin{cases} \text{sinc}(x), & \lvert x \rvert \leq 1, \\ 0, & \text{otherwise}. \end{cases}\end{align}$$

Then $g_L$ is given by

$$\begin{align}g_L(t) = \begin{cases} 1, & \lvert t \rvert \leq l / M, \\ 0, & \text{otherwise}. \end{cases}\end{align}$$

Lanczos filtering is equivalent to replacing $f$ with the local average

$$\begin{align}\hat{f}(t) = \frac{1}{2l / M} \int_{t - l / M}^{t + l / M} f(u) \; \text{d}u.\end{align}$$

The $p$:th order Lanczos filtering is equivalent to repeating this local averaging $p$ times. The $(g_L * \cdots * g_L)$ is a non-negative $(p - 1)$-degree bump polynomial with support $[-lp/M, +lp/M]$. Here is an example with $p = 10$:

Kaiser filter

Another popular choice is the Kaiser filter, defined by

$$\begin{align}G_K(x) = \begin{cases} \frac{I_0(\pi \beta \sqrt{1 - x^2})}{I_0(\pi \beta)}, & \lvert x \rvert \leq 1, \\ 0, & \text{otherwise}, \end{cases}\end{align}$$

where $I_0$ is the zeroth-order Bessel function, and $\beta \in \TR^{\geq 0}$ is a parameter which controls the smoothness of the filter. The $\beta = 0$ corresponds to the brick-wall filter (zeroing terms).

Approximation

We produce an approximation to the reconstructed curve by zeroing out high-frequency Fourier coefficients in the Fourier series. Suppose we use a three-term approximation, with terms -1, 0, +1. The reconstructed curves are then ellipses, and we have something like this:

The way Fourier series is constructed, the approximation with fewer terms is optimal with respect to the parametrization. However, we expect geometric optimality instead; the curve should pass close to the points. We recover geometric approximation by using an arc-length reparametrization:

For fractional shifting, both arc-length reparametrization and noise removal are important for eliminating ringing and retaining a good geometric approximation.

Software

You can find a real-time Python 2.7 program to visualize the fractional Fourier shift from here. The videos on this page have been captured from the program. The program requires NumPy, SciPy, and PyQt to run. Left mouse-button inserts new points. Right mouse-button clears all points.

Remark 1.7.8 - Page generated 01.01.2023 00:19.