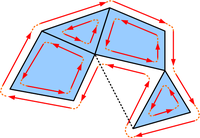
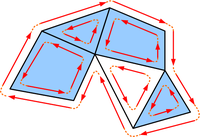
Half-edge structure

01.05.2007 (16.12.2014)

This is a reconstruction of the article I wrote for the comp.graphics.algorithms newsgroup FAQ back in 2007 (or in 2006, can’t remember). The cgafaq had to be taken down after it was filled with spam, so the article was lost. I recovered the latest version cached by the Wayback Machine. It did not have the images, but luckily I had those backed up. Except for the slightly revised writing style, this article follows the original closely.

Introduction

A half-edge structure is a description of the relationships between vertices, half-edges, edges and polygons. In computer graphics, it is used for describing geometric polygon meshes. However, the data structure in itself is just a connectedness description - a topological description.

Many geometric interpretations, called embeddings, can be given to the half-edge structure. The most common interpretation is to map vertices to points, half-edges to directed line segments, edges to line segments and polygons to planar polygons. Another interpretation could map the data structure to a sphere: vertices to points, edges to arcs and polygons to spherical polygons.

What makes the half-edge structure interesting is its ability to efficiently answer such adjacency queries as:

What edges are connected to this vertex?
What polygons are connected to this vertex?
What vertices are connected to this polygon?

and the fact that it achieves this by using only a constant amount of data for each element.

The half-edge structure can describe many of the polygon meshes and all of the graphs (including multigraphs with loops). It can even describe many mixes of a polygon mesh and a wireframe mesh. A wireframe mesh occurs naturally as an intermediate phase when building a polygon mesh: first a polyline is created, and this is then converted to a solid polygon.

There are two important restrictions on the relationships that can be described:

No non-orientable surfaces (e.g. Moebius strip).
No non-manifold surfaces (e.g. two cubes sharing a corner vertex).

The second restriction implies an analogous statement for edges and polygons. The quad-edge structure is a minimal upgrade to the half-edge structure that enables representation of non-orientable surfaces. The partial entity structure extends the idea of halving edges to halving all elements and handles also non-manifold surfaces.

Data structures

Each type of an element carries some connectedness information. For a vertex, an edge, or a polygon, it suffices to give an arbitrary half-edge to which it is connected to. The half-edges are the real source of the connectedness information.

The information seen from a single half-edge.

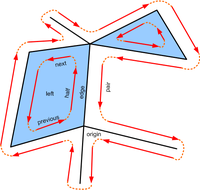
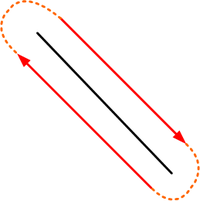
In the following we speak topologically; shapes can be distorted by homeomorphisms. A vertex is a point. A half-edge is a directed line segment, described by an origin vertex and a destination vertex. Each half-edge has a predecessor half-edge and a successor half-edge. The destination vertex of a half-edge is given by the origin vertex of the successor half-edge. The successor (predecessor) half-edges form a loop. This is a natural consequence of the facts that every half-edge must have a successor (predecessor) half-edge and that there are finitely many half-edges. These loops correspond to the boundaries of polygons.

A half-edge is connected to another half-edge, called the pair, which has the same end-vertices but reversed direction. A half-edge is connected to at most one polygon, and to exactly one edge.

These connections can be sketched in C++ as follows:

struct VertexData;
struct EdgeData;
struct PolygonData;

struct HalfData
{
    HalfData* next;
    HalfData* previous;
    HalfData* pair;

    VertexData* origin;
    PolygonData* left;
    EdgeData* edge;
};

struct VertexData
{
    HalfData* half;
};

struct EdgeData
{
    HalfData* half;
};

struct PolygonData
{
    HalfData* half;
};

Example usage

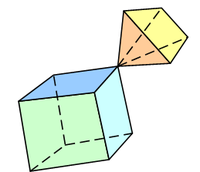
The commonly needed operations with a half-edge structure include traversing the edges around a vertex or traversing the edges around a polygon. You can examine how the traversal is done by comparing the code and the image above.

Traversing the edges around a vertex

if (vertex.half != 0)
{
    HalfData* begin = vertex.half;
    HalfData* half = begin;
    do
    {
        // Do something.
        half = half->pair->next;
    }
    while(half != begin);
}

For abstraction, it might be useful to form the following functions:

vertexNext(half) := half->pair->next
vertexPrev(half) := half->previous->pair

Traversing the edges around a polygon

if (polygon.half != 0)
{
    HalfData* begin = polygon.half;
    HalfData* half = begin;
    do
    {
        // Do something.
        half = half->next;
    }
    while(half != begin);
}

Variants

The half-edge structure has many variants depending on the amount of information used and how it is organized.

Generality vs memory

Vertices can be left out. Edges can be left out. Polygons can be left out. The only necessary information is the half-edges. In this article we treat the most general case.

Data organization

In the half-edge, you could store the destination vertex instead of the origin vertex as well as store the right polygon instead of the left polygon. You could store vertexNext and vertexPrev fields instead of the next and previous fields. Given any two fields of these four, the left out fields can be deduced in constant time. If only one of the fields is given, then one of the left out fields can be deduced in constant time and the other two in linear time.

We define half-edges with the origin vertex, the left polygon, the successor half-edge, and the predecessor half-edge.

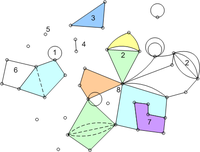
Representable polygon meshes

Half-edge structure can represent the following combinations of adjacencies:

Edge loops*
Multi-edges*
Isolated polygons
Isolated edges
Isolated vertices
Mixed wireframe and polygon meshes*
Polygons with an arbitrary number of vertices and edges
Polygons meeting only at one vertex

The * star denotes that the listed item is not always representable.

A half-edge structure embedded on the plane. A dashed edge denotes disjointness from the underlying polygon.

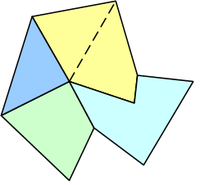
Non-representable polygon meshes

A half-edge path is a sequence of half-edges (h_1, …, h_n), such that destination(h_i) = origin(h_{i + 1}), for all i in [1, n]. The half-edge path is a loop, if destination(h_n) = origin(h_1). The half-edge loop is properly oriented, if polygon(h_i) = polygon(1), for all i in [1, n]. A half-edge is reserved, if polygon(h) exists. A half-edge which is not reserved, is free. A vertex is reserved, if all of its outgoing half-edges are reserved. Otherwise the vertex is free.

A non-representable edge in 3D.

A non-representable vertex at the lower vertex of the wireframe edge in 2D.

A non-representable vertex at the join of the closed meshes in 3D.

The restrictions for the half-edge structure are:

An edge can be added between vertices A and B if and only if A and B are free.
A half-edge loop can be turned to a polygon if and only if every half-edge in the loop is free and the loop can be made properly oriented by reordering the connectivity around the vertices of the loop.

The second statement (among other things) excludes the representation of non-orientable surfaces, such as the Moebius strip. Both statements together exclude many of the non-manifold meshes (but see the discussion below).

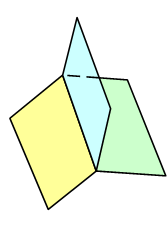
The reordering mentioned in the second statement is important in that it enables the representation of polygons that are connected only by one vertex, for example a propel. This situation arises frequently when building a polygon model.

Non-manifold edges

Could we represent non-manifold edges with the half-edge structure? This sounds plausible if we relax the requirement for a half-edge to be the pair of its pair . Then the half-edge pairs would form a singly-linked list around the shared edge. The good and the bad news are the same: it works in half of the cases. However, these cases are interleaved, and as such is not at all practical.

A non-manifold edge at the join of more than two polygons in 3D.

An even number of polygons sharing an edge is representable, while an odd number of polygons is not. To get to the four-polygon case requires to go through the three-polygon case, which is not representable.

If such non-manifold conditions need to be represented, one should consider more advanced data structures, such as the partial entity structure.

Design decisions

There are many ways to implement the half-edge structure. They differ both in capability of representing different kinds of meshes, in the ease of use and in the ease of implementation. This article represents an implementation strategy that does well in all of these areas.

Goals

Algorithms must make it possible to represent the widest possible set of different polygon meshes that the half-edge structure can represent.
Algorithms must be easy to understand.

Marking the boundary of the mesh

Isolated vertices are represented by their half-edge being null. Boundary half-edges are marked with a null left polygon.

In particular, a null pair should not be used to mark the boundary; otherwise the data structure cannot traverse around the vertices correctly.

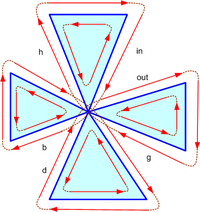
Making two half-edges adjacent

Given is a half edge A arriving at vertex V, and a half edge B leaving from V. We would like to order, if possible, the neighbourhood of V such that A is a predecessor of B (B.previous = A) and B is a successor of A (A.next == B).

A mesh before calling makeAdjacent(in, out).

A mesh after calling makeAdjacent(in, out).

For this to make sense, A and B must both be free (A.left = B.left = null). Reordering the neighbourhood is required when adding a polygon. Because we want to connect A and B together, the link chain around V must be cut at A.next and B.previous. These two half-edges denote a region around V. This region was between A and B, but now it has to be moved between two other successive, free half-edges, say G and H (H = g.next). If there is no such half-edge G, the reordering is not possible.

bool HalfMesh::makeAdjacent(Half in, Half out)
{
    if (in.next() == out)
    {
        // Adjacency is already correct.

        return true;
    }

    Half b(in.next());
    Half d(out.previous());

    // Find a free incident half edge
    // after 'out' and before 'in'.
    Half g(findFreeIncident(out.origin(), 
        out.pair(), in));
    if (g.empty())
    {
        // There is no such half-edge.
        return false;
    }
    Half h(g.next());

    in.half_->next_ = out.half_;
    out.half_->previous_ = in.half_;

    g.half_->next_ = b.half_;
    b.half_->previous_ = g.half_;

    d.half_->next_ = h.half_;
    h.half_->previous_ = d.half_;

    return true;
}

Adding a vertex

Allocate the vertex.
Set the vertex’s half-edge to null.

Adding an edge

Allocate an edge.
Allocate two half-edges.
Initialize the half-edges to be paired and linked to each other.
Associate the half-edges with the edge and vice versa.
Link one side of the edge to the mesh.
Link the other side of the edge to the mesh.

An initialized edge before its addition to the mesh.

A mesh before adding an edge.

A mesh after adding an edge.

Edge HalfMesh::addEdge(Vertex fromVertex, 
                       Vertex toVertex)
{
   // Decide what to do with loop edges.
   bool loopEdges = true;
   if (!loopEdges)
   {
      if (fromVertex == toVertex)
      {
         return Edge();
      }
   }

   // Decide what to do with parallel edges.
   bool parallelEdges = true;
   if (!parallelEdges)
   {
      Half existingHalf(findSomeHalf(fromVertex,
         toVertex));

      if (!existingHalf.empty())
      {
         return existingHalf.edge();
      }
   }

   // Allocate data

   Edge edge(allocateEdge());
   Half fromToHalf(allocateHalf());
   Half toFromHalf(allocateHalf());

   // Initialize data

   {
      EdgeData* edgeData = edge.edge_;
      edgeData->half_ = fromToHalf.half_;
   }

   {
      HalfData* halfData = fromToHalf.half_;

      halfData->next_ = toFromHalf.half_;
      halfData->previous_ = toFromHalf.half_;
      halfData->pair_ = toFromHalf.half_;
      halfData->origin_ = fromVertex.vertex_;
      halfData->edge_ = edge.edge_;
      halfData->left_ = 0;
   }

   {
      HalfData* halfData = toFromHalf.half_;

      halfData->next_ = fromToHalf.half_;
      halfData->previous_ = fromToHalf.half_;
      halfData->pair_ = fromToHalf.half_;
      halfData->origin_ = toVertex.vertex_;
      halfData->edge_ = edge.edge_;
      halfData->left_ = 0;
   }

   // Link the from-side of the edge.

   if (fromVertex.isolated())
   {
      VertexData* vertexData = fromVertex.vertex_;
      vertexData->half_ = fromToHalf.half_;
   }
   else
   {
      Half fromIn(findFreeIncident(fromVertex));
      Half fromOut(fromIn.next());

      fromIn.half_->next_ = fromToHalf.half_;
      fromToHalf.half_->previous_ = fromIn.half_;

      toFromHalf.half_->next_ = fromOut.half_;
      fromOut.half_->previous_ = toFromHalf.half_;
   }

   // Link the to-side of the edge.

   if (toVertex.isolated())
   {
      VertexData* vertexData = toVertex.vertex_;
      vertexData->half_ = toFromHalf.half_;
   }
   else
   {
      Half toIn(findFreeIncident(toVertex));
      Half toOut(toIn.next());

      toIn.half_->next_ = toFromHalf.half_;
      toFromHalf.half_->previous_ = toIn.half_;

      fromToHalf.half_->next_ = toOut.half_;
      toOut.half_->previous_ = fromToHalf.half_;
   }

   return edge;
}

Adding a polygon

Check that the data is valid and that the given half-edge loop can be turned into a polygon as given by the required conditions.
Reorder the links such that the given half-edge loop becomes sequential, ie. that the next-field of one half-edge points to the next half-edge in the loop (similarly for previous-fields).
Create the polygon.
Connect the polygon to an arbitrary boundary half-edge.
Connect each boundary half-edge to the polyogn.

Polygon HalfMesh::addPolygon(const std::vector<Half>& halfLoop)
{
   if (halfLoop.empty())
   {
      return Polygon();
   }

   integer halfCount = halfLoop.size();

   // Check that the half-edges are free
   // and form a chain.

   for (integer i = 0;i < halfCount;++i)
   {
      integer nextIndex = i + 1;
      if (nextIndex == halfCount)
      {
         nextIndex = 0;
      }

      Half current(halfLoop[i]);
      Half next(halfLoop[nextIndex]);

      if (current.destination() != next.origin())
      {
         // The half-edges do not form a chain.
         return Polygon();
      }
      if (!current.isFree())
      {
         // The half-edge would introduce a
         // non-manifold condition.
         return Polygon();
      }
   }

   // Try to reorder the links to get
   // a proper orientation.

   for (integer i = 0;i < halfCount;++i)
   {
      integer nextIndex = i + 1;
      if (nextIndex == halfCount)
      {
         nextIndex = 0;
      }

      if (!makeAdjacent(halfLoop[i], halfLoop[nextIndex]))
      {
         // The polygon would introduce a non-manifold
         // condition.
         return Polygon();
      }
   }

   // Create the polygon

   Polygon newPolygon(allocatePolygon());

   // Link the polygon to a half-edge

   PolygonData* polygonData = newPolygon.polygon_;
   polygonData->half_ = halfLoop[0].half_;

   // Link half-edges to the polygon.

   for (integer i = 0;i < halfCount;++i)
   {
      Half current(halfLoop[i]);

      HalfData* halfData = current.half_;
      halfData->left_ = newPolygon.polygon_;
   }

   return newPolygon;
}

Removing a polygon

Set the polygon of each boundary half-edge to null.
Deallocate the polygon.

void HalfMesh::removePolygon(Polygon polygon)
{
   Half begin(polygon.half());
   Half current(begin);

   do
   {
      HalfData* halfData = current.half_;
      halfData->left_ = 0;
      current = current.next();
   } 
   while(current != begin);

   deAllocatePolygon(polygon);
}

Removing an edge

Remove all of the polygons connected to the edge.
Link the half-edges of the edge off from the mesh.
Deallocate the edge and its half-edges.

bool HalfMesh::removeEdge(Edge edge)
{
   Half fromToHalf(edge.half());
   Half toFromHalf(fromToHalf.reverse());

   // Remove the neighbouring polygons.

   if (!fromToHalf.left().empty())
   {
      removePolygon(fromToHalf.left());
   }

   if (!toFromHalf.left().empty())
   {
      removePolygon(toFromHalf.left());
   }

   // Link the from-side of the edge
   // off the model.

   Vertex fromVertex(fromToHalf.origin());

   Half fromIn(fromToHalf.previous());
   Half fromOut(fromToHalf.rotateNext());

   if (fromVertex.half() == fromToHalf)
   {
      if (fromOut == fromToHalf)
      {
         fromVertex.vertex_->half_ = 0;
      }
      else
      {
         fromVertex.vertex_->half_ = fromOut.half_;
      }
   }

   fromIn.half_->next_ = fromOut.half_;
   fromOut.half_->previous_ = fromIn.half_;

   // Link the to-side of the edge
   // off the model.

   Vertex toVertex(toFromHalf.origin());

   Half toIn(toFromHalf.previous());
   Half toOut(toFromHalf.rotateNext());

   if (toVertex.half() == toFromHalf)
   {
      if (toOut == toFromHalf)
      {
         toVertex.vertex_->half_ = 0;
      }
      else
      {
         toVertex.vertex_->half_ = toOut.half_;
      }
   }

   toIn.half_->next_ = toOut.half_;
   toOut.half_->previous_ = toIn.half_;

   // 3) Deallocate data

   deAllocateHalf(fromToHalf);
   deAllocateHalf(toFromHalf);
   deAllocateEdge(edge);
}

Removing a vertex

Remove all of the edges connected to the vertex.
Deallocate the vertex.

void HalfMesh::removeVertex(Vertex vertex)
{
   if (!vertex.isolated())
   {
      // Remove every edge that is connected
      // to this vertex

      Half current;
      Half next(vertex.half());

      do
      {
         current = next;
         next = next.rotateNext();
         // Avoid removing the same edge
         // twice in case of an edge loop.
         if (next.edge() == current.edge())
         {
            next = next.rotateNext();
         }
         removeEdge(current.edge());
      }
      while(current != next);
   }

   deAllocateVertex(vertex);
}