Point kd-tree
A point kd-tree is a tree data-structure for storing a finite set of points such that nearest neighbors can be found efficiently.
Traversal of the subdivision using cursors
The nodes of the kd-tree are traversed using cursors. From each node you can traverse either to a parent (if it exists) or to left or right child (if they exist). At each node you can inspect:
-
How many points are stored under the sub-tree whose root-node the current node is?
-
What those points are? (iterator range to the point list).
-
What are the node bounds on the splitting dimension?
-
What are the cursors to the child nodes?
-
What is the cursor to the parent node?
Features
-
The points stored in the kd-tree are traversed through an iterator interface. Note that their order can change after subdivision, and if a point is removed and immediately inserted back, it might take another position in the point list.
-
Points can be inserted into the tree at any time, either one by one or as a set. No new nodes are created in this process.
-
Points can be removed from the tree at any time. This can be done either one by one, or by removing all points at once.
-
The recursive subdivision of the kd-tree can be refined at any time. In this process existing leaf nodes are converted into split nodes by recursively subdividing them into two new leaf nodes. The split plane is chosen by a splitting rule.
-
Each split node contains the bounds of the node on the splitting axis. Knowing these bounds is essential in the implementation of an efficient nearest neighbor searching algorithm.
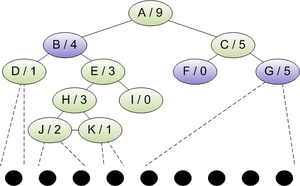
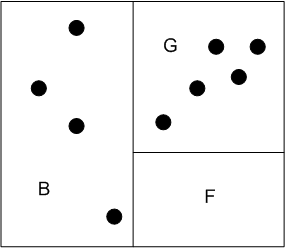
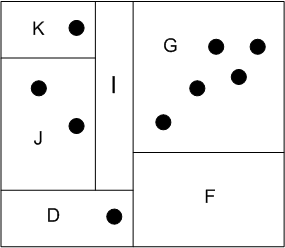
Illustration
The image below illustrates the multi-level kd-tree in .
See also
Nearest neighbors in semi-dynamic point sets